Regresní přímka v maticovém vyjádření

V předchozí kapitole regresní přímka a Cramerovo pravidlo je demonstrován odhad b_j neznámých parametrů β_j modelu regresní přímky pomocí Cramerova pravidla. Nyní je na programu druhý a asi nejčastěji používaný způsob odhadu parametrů. Tím způsobem je maticové vyjádření klasického lineárního regresního modelu a odhad parametrů modelu pomocí bodové odhadové funkce metody nejmenších čtverců (MNČ) ve tvaru b = (X^TX)^-1X^Ty.

Bodová odhadová funkce MNČ

Výchozím bodem odvození odhadové funkce MNČ je vyjádření KLRM v maticové podobě.

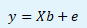
y ... sloupcový vektor n pozorování hodnot závisle proměnné
X ... matice n x (k + 1) pozorování hodnot vysvětlujících proměnných
b ... sloupcový vektor k + 1 neznámých parametrů
e ... sloupcový vektor n náhodných složek → e = y - Xβ

Minimalizační kritérium MNČ lze obecně pro KLRM zapsat v následujícím tvaru.

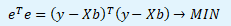
Kritérium minimalizuje součet čtverců odchylek reziduální složky. Parciální derivací minimalizační kritéria podle vektoru b^T a položením rovno nule získáme soustavu normálních rovnic.

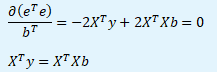
Posledním krokem je vyjádření odhadové funkce b ze soustavy normálních rovnice.

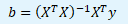
Odhad parametrů regresní přímky

Výchozím bodem odhadu vektoru parametrů b KLRM je následující maticový zápis modelu včetně jeho rozepsání.

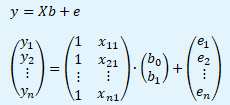
Jedničkový sloupec v matici nezávisle proměnných X představuje hodnoty pro odhad parametru b₀. Pokud by byl odhadován model bez úrovňové konstanty, jedničkový sloupec by v matici nefiguroval.

Vektor hodnot závisle proměnné y a matici hodnot nezávisle proměnných X postupně upravíme do podoby bodové odhadové funkce MNČ. První krokem je převod matice X na transponovanou matici X^T a jejich vzájemný součin.

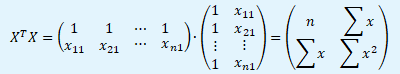
Dále je potřeba vytvořit inverzní matici (X^TX)^-1 k matici (X^TX). Výpočet inverzní matice se provádí pomocí transformace přes jednotkovou matici. Pro udržení jednoduchosti si pomůžeme v MS Excel pomocí maticové funkce INVERZE().

Jednotková matice je taková matice, která má na hlavní diagonále samé jedničky a ostatní prvky mimo ní jsou nulové.

Transponovanou matici X^T nezávisle proměnných vynásobíme vektorech hodnot závisle proměnné y.

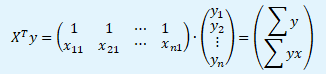
Posledním krokem je součin vypočtených matic (X^TX)^-1 a X^Ty, abychom získali odhad vektoru b regresních parametrů.

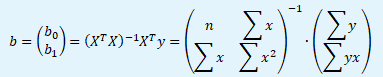
Maticový odhad regresních parametrů v praxi

Cílem článku je odhad parametrů b_j výběrové regresní přímky ve tvaru Y = b₀ + b₁x. V následující tabulce máme k dispozici empirická data průměrných měsíčních spotřebních výdajů a příjmu spotřebitele v jednotlivých letech. Úkolem je kvantifikovat vztah mezi spotřebními výdaji y a příjmem spotřebitele x.

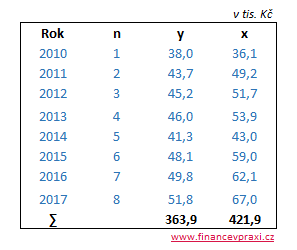
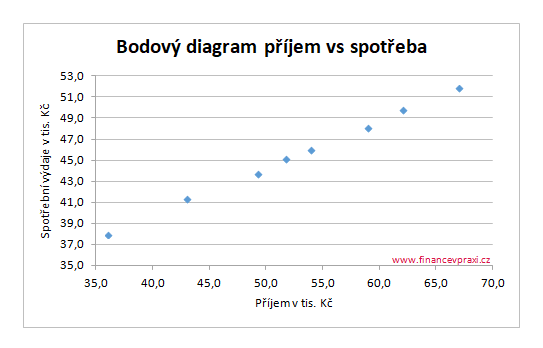
Z předchozího článku Regresní přímka a Cramerovo pravidlo již víme, že mezi proměnnými je lineární vztah, který můžeme vyjádřit pomocí regresní přímky.

V prvním kroku naplníme vektor y a matici X hodnotami z tabulky.

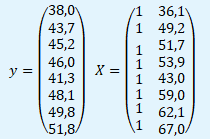
Součin matic si můžete usnadnit v MS Excel pomocí maticové funkce SOUČIN.MATIC(). Inverzní funkci vypočtete pomocí již zmíněné funkce INVERZE().

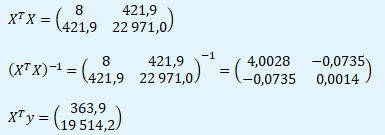
Nyní již můžeme odhadnout regresní parametry pomocí bodové odhadové funkce MNČ ve tvaru b = (X^TX)^-1X^Ty.

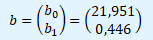
Na základě odhadů parametrů b₀ a b₁ nyní můžeme sestavit výběrovou regresní funkci Y v indexovém tvaru.

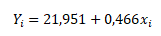
Když máme odhady parametrů modelu, můžeme za x_i dosadit jednotlivé hodnoty nezávisle proměnné a dopočítat vyrovnané hodnoty Y.

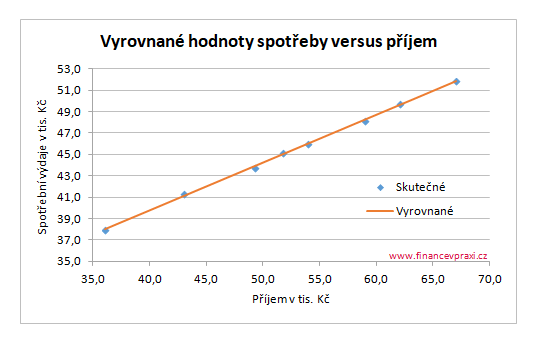
Srovnejte odhady parametrů b₀ a b₁ výběrové regresní přímky s odhady z článku Regresní přímka a Cramerovo pravidlo.