Regresní přímka a Cramerovo pravidlo

Kdejaká odborná kniha obsahuje vzorce pro výpočet výběrových odhadů parametrů regresní přímky. Pro zvídavější čtenáře to nemusí být dostačující. Proto jsem se rozhodnul napsat příspěvek, který obsahuje detailní postup, jak se k takovým vzorcům dostat.

Příspěvek obsahuje řešení minimalizačního kritéria MNČ a řešení soustavy rovnic pomocí Cramerova pravidla.

Soustava rovnic pro regresní přímku

Vycházet budu z regresní přímky

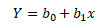
Y ... vyrovnané hodnoty závisle proměnné, x ... empirické hodnoty nezávisle proměnné, b₀ a b₁ ... odhady výběrových parametrů

Prvním krokem pro sestavení soustavy normálních rovnic je řešení minimalizačního kritéria metody nejmenších čtverců pro danou výběrovou regresní funkci

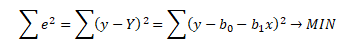
Parciálními derivacemi minimalizačního kritéria podle jednotlivých parametrů získáme rovnice

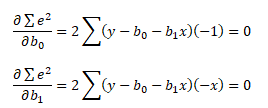
ze kterých vytvoříme finální podobu soustavy rovnic o 2 neznámých regresních parametrech b₀ a b₁

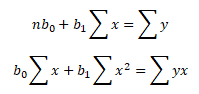
Analogicky lze získat soustavu rovnic pro všechny ostatní regresní funkce.

Cramerovo pravidlo

Cramerovo pravidlo je jednou z metod, která se používá k řešení soustavy algebraických rovnic. V našem konkrétním případě hledáme řešení pro neznámé parametry b₀ a b₁.

Ze soustavy normálních rovnic vytvoříme matici A, která obsahuje všechny prvky z levé strany soustavy rovnic. A vektor pravých stran z prvků na pravé straně soustavy.

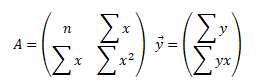
Dále z matice A vytvoříme matice A_i pro jednotlivé parametry, které vzniknou nahrazením i-tého sloupce matice vektorem pravých stran

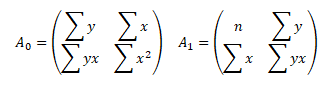
Je-li determinant matice A je nenulový (značeno detA ≠ 0), pak má soustava jedno řešení. To znamená, že pro jednotlivé parametry existuje jedno řešení dáno Cramerovým vzorcem

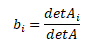
b_i ... hledaný i-tý neznámý parametr, detA_i ... determinant matice A_i, detA ... determinant matice A

Determinant matice je reálné číslo, které je určitým algoritmem přiřazeno čtvercové matici (n x n). Algoritmus se pro každý řád čtvercové matice liší.

Determinant čtvercové matice řádu n = 2 je dán rozdílem součinů prvků daných křížovým pravidlem

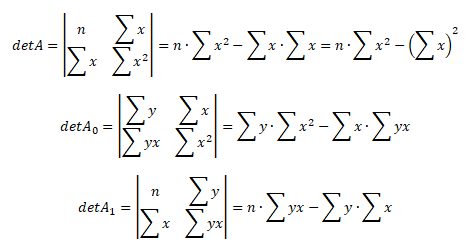
Posledním krokem je dosazení do Cramerova vzorce pro výpočet odhadů regresních parametrů

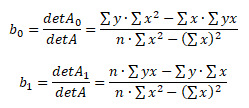
Odhad neznámých parametrů v praxi

K dispozici máme empirická data o průměrném měsíčním příjmu a spotřebních výdajích jednotlivce v jednotlivých letech. Zajímá nás kvantitativní vztah mezi uvedenými proměnnými. Závisle proměnnou y jsou spotřební výdaje a nezávisle proměnnou x je čistý příjem.

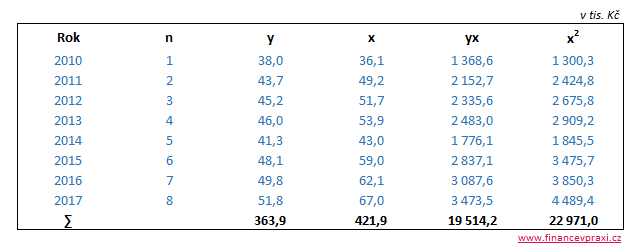
Následující tabulka obsahuje proměnné potřebné pro řešení soustavy normálních rovnic n, x, y a vytvořené proměnné x² a yx.

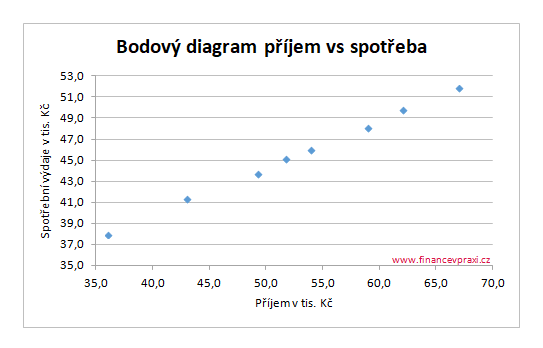
Průběh závislosti mezi 2 proměnnými lze identifikovat pomocí bodového diagramu, který ukazuje na lineární vztah.

Soustava normálních rovnic pro odhad parametrů regresní přímky má následující konkrétní podobu, kde sumační hodnoty jsou převzaty ze sumačního řádku tabulky

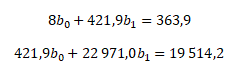
Ze soustavy rovnic vytvořime matici A a vypočteme její determinant pomocí křížového pravidla

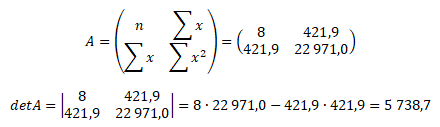
Determinant matice A je různý od nuly. To znamená, že soustava rovnic má řešení a můžeme pokračovat.

Z matice A a vektoru pravých stran vytvoříme matici A₀ a vypočteme její determinant

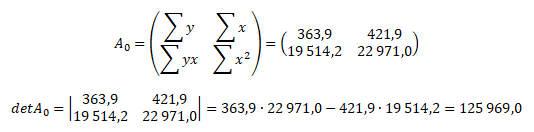
Stejným způsobem vytvoříme matici A₁ a vypočteme determinant

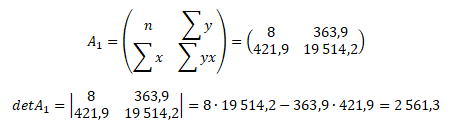
Posledním krokem je výpočet neznámých parametrů b₀ a b₁ regresní přímky pomocí Cramerových vzorců

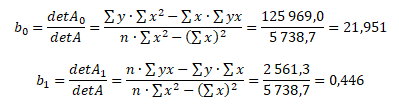
Na základě výběrových odhadů b₀ a b₁ neznámých parametrů β₀ a β₁ nyní můžeme sestavit výběrovou regresní funkci Y v indexním tvaru

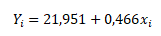
a dále pak pro konkrétní hodnoty x_i dopočítáme vyrovnané hodnoty regresní přímky

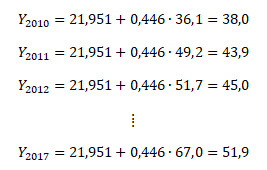
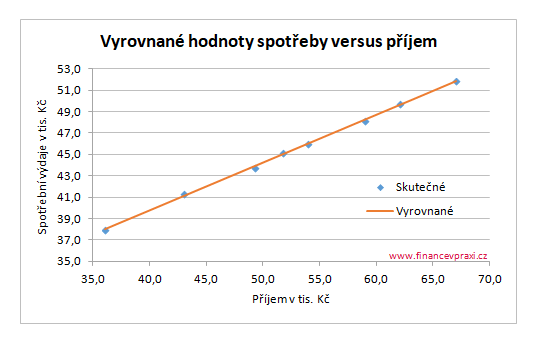
Vyjádříme-li spotřební funkci jako stochastickou závislost skutečných hodnot závisle proměnné y na výběrové regresní přímce Y a reziduální složce e, pak můžeme dopočítat reziduální složku modelu rozdílem mezi skutečnou hodnotou a vyrovnanou hodnotou

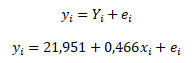
Reziduální složku pak můžeme testovat z hlediska sériové nezávislosti a konstantního rozptylu (předpoklady MNČ).