Kovariance a korelace příklady

Kovariance a korelace slouží k vyjádření vzájemné závislosti náhodných veličin. V případě zkoumání závislosti mezi více než 2 veličinami jsou koeficienty kovariance a korelace uspořádány do kovarianční a korelační matice.

Cílem kapitoly je výpočet párových koeficientů kovariance a korelace a sestavení kovarianční a korelační matice.

Výpočet koeficientů závislosti a sestavení matic

Akciový trh je reprezentován váženým akciovým indexem. Index je vážen tržní kapitalizací 5 kótovaných společností - akcie A (30 %), akcie B (12 %), akcie C (8 %), akcie D (21 %) a akcie E (29 %).

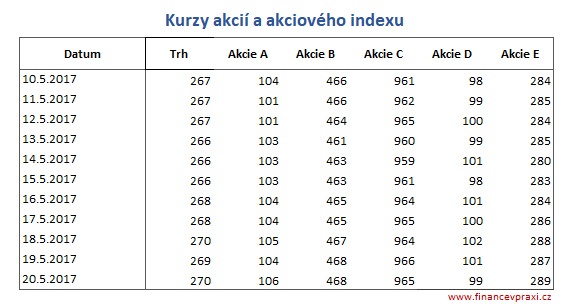
Z tržních kurzů akcií a indexu jsou vypočteny denní změny v procentech. Z nich jsou pak vypočteny průměrné výnosnosti, rozptyly výnosností, směrodatné odchylky a variační koeficienty.

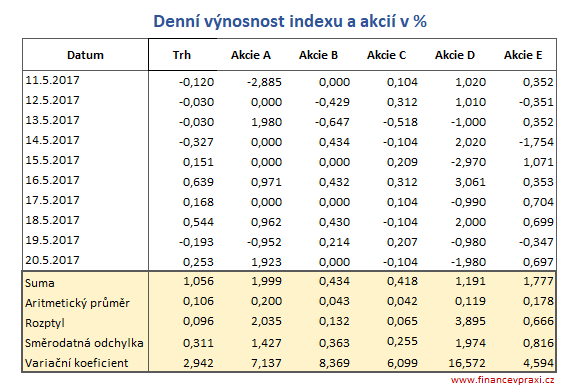
Variační koeficient poměřuje riziko akcie měřené směrodatnou odchylkou a průměrnou výnosnost měřenou aritmetickým průměrem. Variační koeficient říká, kolik % rizika připadá na 1 % výnosnosti. Nejlépe vychází akcie E s variačním koeficientem 4,594 a nejhůře akcie D s 16,572.

a) Vypočet vybraných kovariancí z denních výnosností

Kovariance akciového indexu a kurzu akcie A

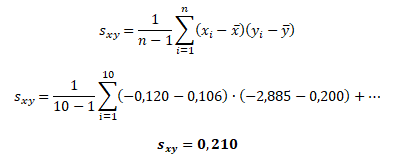
a kovariance samotného akciového indexu

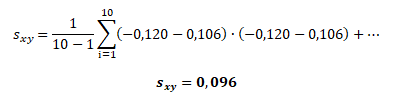
b) Vypočet vybraných korelačních koeficientů

Korelace indexu a akcie A

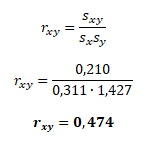
a korelace samotného indexu

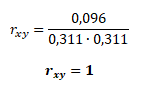
Stejným způsobem by se postupovalo pro všechny ostatní koeficienty kovariance a korelace.

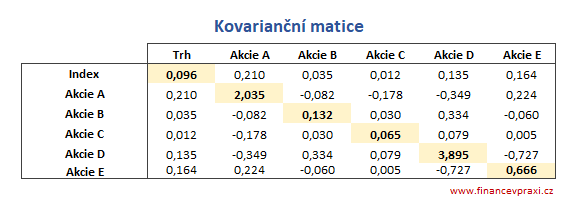
c) Sestavení kovarianční matice

Hodnoty kovariancí na diagonále musí být rovny rozptylu denních výnosností jednotlivých akcií a indexu. Hodnoty na diagonále kovarianční matice tedy slouží jako kontrola správnosti vypočtených kovariancí.

d) Sestavená korelační matice

Jako kontrola správnosti vypočtených korelačních koeficientů uspořádaných do korelační matice slouží hodnoty na diagonále matice. Hodnoty na diagonále korelační matice musí být rovny jedné.

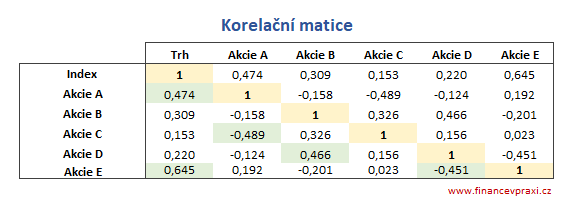
V korelační matici jsou barevně zvýrazněny významné korelační koeficienty, tj. |r_xy| > 0,4. Koeficient korelace 0,645 vypovídá o poměrně silné přímé závislosti mezi akciovým indexem a tržní cenou akcie E. Naopak koeficient korelace -0,489 vypovídá o poměrně silném negativním vztahu akcií A a C.