Úvod do posloupností
Publikováno: 9.4.2019

Princip posloupnosti, graf posloupnosti, způsoby zadání posloupnosti, základní druhy posloupnosti
- posloupnost
- funkce
- přirozená čísla
Posloupnost je uspořádaná řada čísel generovaná funkcí, která každému přirozenému číslu n přiřadí reálné číslo an. Posloupnost je speciální případ reálné funkce, jejímž definičním oborem je množina přirozených čísel N a oborem funkčních hodnot množina reálných čísel R.
Nekonečná a konečná posloupnost
Hned na začátku je potřeba zmínit dvě základní vlastnosti posloupností. Posloupnosti se rozlišují podle toho, zda jsou či nejsou omezené na definičním oboru.
Je-li posloupnost definovaná na množině všech přirozených čísel je posloupnost nekonečná a zapisuje se jako
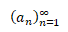
Je-li naopak posloupnost definovaná konečným počtem prvků k z množiny přirozených čísel je posloupnost konečná a zapisuje se jako
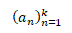
Princip posloupnosti
Princip posloupnosti si ukážeme na jednoduchém příkladu nekonečné posloupnosti zadané pro n-tý člen
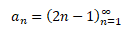
Vypíšeme si prvních pět členů posloupnosti tak, že každému přirozenému číslu n, tj. 1, 2, 3, ..., přiřadíme reálné číslo an na základě zadaného funkčního předpisu, tj. a1, a2, a3, ...
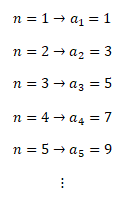
Z příkladu by mělo být jasně patrné, že jsme očíslovali jednotlivé členy posloupnosti přirozenými čísly. Posloupnost tedy není nic jiného než očíslovaná řada reálných čísel. Důležité je vždy zachovat pořadí členů.
Graf posloupnosti
Grafem posloupnosti není spojitá křivka jako je tomu u reálných funkcí, ale uspořádaná n-tice izovalovaných bodů se souřadnicemi [n,an]. Graf prvních pěti členů výše zadané nekonečné posloupnosti
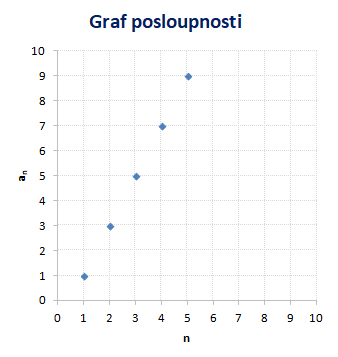
Zápis posloupnosti
Posloupnost se zapisuje dvěma způsoby. První způsob zápisu již byl zmíněn, tj. posloupnost zadaná pomocí vzorce pro n-tý člen
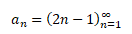
Druhým způsobem je rekurentní zadání posloupnosti, kdy je zadán první člen a1 nebo několik prvních členů posloupnosti a vzorec pro výpočet následujících hodnot an + 1
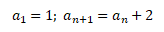
Rekurentně zadaná posloupnost se řeší postupným dosazováním předchozí hodnoty do zadaného vzorce
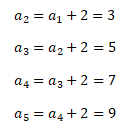
Převod na rekurentní zápis
Oba zápisy jsou identické, neboť vedou ke stejné řadě čísel. Chceme-li posloupnost zadanou pro n-tý člen vyjádřit rekurentně, musíme původní vzorec pro an vyjádřit pro následující člen an + 1
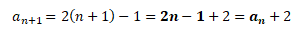
Druhy posloupnosti
Rozlišují se dva základní druhy posloupností - aritmetická a geometrická posloupnost. V názvech posloupností se skrývají zákonitosti, kterými jsou generovány jejich hodnoty.
Aritmetická posloupnost
Každý člen posloupnosti an (počínaje druhým členem) je aritmetickým průměrem sousedních členů
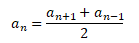
Geometrická posloupnost
Každý člen posloupnosti an (počínaje druhým členem) je geometrickým průměrem absolutních hodnot sousedních členů
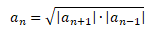
- ODVÁRKO. O.: Matematika pro gymnázia. Posloupnost a řady. Prometheus 1995, Praha. Dotisk třetího vydání, 126 stran. ISBN 978-80-7196-391-2
- POLÁK, J.: Přehled středoškolské matematiky. PROMETHEUS 2015, Praha. Desáté vydání, 659 stran. ISBN 978-80-7196-458-2
- RADOVÁ, J., DVOŘÁK, P.: Finanční matematika pro každého. GRADA Publishing 2003, Praha. Čtvrté rozšířené vydání, 260 stran. ISBN 80-247-0473-0

