Výnos a riziko akcie

Akcie jsou v dlouhodobém horizontu bezesporu nejvýnosnější třídou aktiv. Výnosnost akcií však nelze sledovat odděleně od jejich rizika. Riziko akcií spočívá v kolísání tržních cen a výnosů.

Akcie a její hodnota

Akcie je majetkový cenný papír, který zakládá podíl na majetku společnosti. S držbou akcií je spojeno právo podílet se na řízení společnosti, právo podílet se na zisku a právo na likvidačním zůstatku.

Akcie zní na určitou nominální hodnotu (jmenovitou hodnotu), která vyjadřuje podíl akcionáře na základním kapitálu společnosti. Převis emisní hodnoty akcie nad její nominální hodnotou se označuje jako emisní ážio.

Tržní cena (P) veřejně obchodované akcie je dána poptávkou a nabídkou na burze cenných papírů, tj. zájmem investorů. Rizikovost akcie se odráží v kolísání tržní ceny. Důvody kolísání jsou změny očekávání investorů, vývoj podnikových fundamentálních faktorů (zisk na akcii, zadlužení společnosti, růst tržeb apod.), vývoj makroekonomického a politického prostředí a psychologická nálada trhu.

Pro investory je velmi důležitá vnitřní hodnota akcie. Vnitřní hodnota představuje teoretickou cenu akcie, kterou jí investoři na základě očekávaného peněžního toku přisoudí. Akcie může mít tolik vnitřních hodnot, kolik je investorů.

Tržní cena vs vnitřní hodnota akcie

Porovnání cen	Hodnocení akcie	Investiční doporučení
P > V	nadhodnocená	nekupovat
P = V	správně oceněná	držet
P < V	podhodnocená	koupit

Vnitřní hodnotu akcie lze odhadnout například pomocí dividendových diskontních modelů (Gordonův model, třístupňový DDM atd.). DDM modely však nejsou použitelné pro společnosti, které nevyplácí dividendy. Pro tyto společnosti lze použít ziskové modely a modely diskontovaného cashflow. Nevýhodou uvedených modelů je citlivost na vstupní údaje, které jsou do značné míry záležitostí subjektivního názoru investora.

Výnos jako náhodná veličina

Výnosy akcií jsou náhodné veličiny, na které můžeme pro jednoduchost nahlížet jako na diskrétní náhodné veličiny. Výnosy akcií se tedy mění v jednotlivých diskrétních krocích, které odpovídají jednotlivým obchodním dnům. Diskrétní náhodná veličina je definována pomocí pravděpodobnostní funkce, která udává s jakou pravděpodobností p(x_i) jsou realizovány konkrétní hodnoty x_i výnosu akcie.

Obecně lze náhodnou veličinu charakterizovat pomocí střední hodnoty E(X), rozptylu D²(X) a směrodatné odchylky D(X).

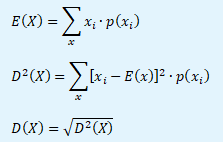
V praxi není pravděpodobností struktura výnosu a rizika akcie známa. Je založena na expertních odhadech.

Vzhledem k tomu, že nás zajímá výnosnost a riziko ex post, nemusíme si s pravděpodobnostní strukturou budoucích výnosů a rizik lámat hlavu. Ve všech případech za p(x) dosadíme jedničku.

Výnosnost akcie za dobu držení

V souvislosti s investováním do akcií (i do jiných druhů aktiv) může investor získat 2 druhy výnosů - kapitálový a důchodový výnos.

Kapitálový výnos vyplývá ze změny tržní ceny akcie. Investor realizuje kapitálový zisk (cena prodej > cena nákup), popřípadě kapitálovou ztrátu (cena prodej < cena nákup) prodejem akcie.

Důchodový výnos z akcie představuje pravidelně se opakující platby ve formě dividend. Výplata dividend je výsledkem dividendové politiky společnosti.

Součet obou výnosů se označuje jako absolutní výnos z akcie. Abstrahujeme-li od daní a transakčních poplatků, můžeme absolutní výnos vyjádřit jako

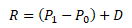
kde R je hrubý výnos akcie, P₁ je prodejní cena akcie, P₀ je nákupní cena akcie, D je dividenda na akcii

Výnos akcie (i jiné investice) se nejčastěji vyjadřuje relativně v podobě výnosové míry. Výnosová míra vyjadřuje rentabilitu investovaného kapitálu

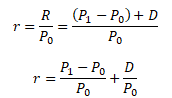
kde r je výnosová míra akcie, (P₁ - P₀)/P₀ je kapitálová výnosnost, D/P₀ je dividendová výnosnost

Výnosová míra může být dále upravena o zdanění kapitálového a dividendového výnosu a transakční náklady spojené s nákupem a prodejem akcií

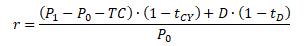
kde TC jsou transakční náklady, t_CY je daňová sazba pro zdanění kapitálového zisku a t_D je daňová sazba pro zdanění dividend

Roční výnosnost akcie

Dosud jsme uvažovali výpočet výnosnosti akcie za celou dobu držení. V praxi jsou však akcie drženy kratší nebo delší dobu než jeden rok. Proto se výnosnost přepočítává na roční bázi, aby jí bylo možné porovnávat s jinými výnosovými mírami na finančním trhu (například s dluhopisy, podílovými fondy apod.), mírou inflace apod.

Roční výnosnost bez reinvestice výnosů se počítá na principu jednoduchého úročení pomocí vzorce

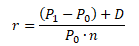
kde n je doba držby akcií v letech, n = 3/12 (držba akcií 3 měsíce), n = 15/12 (držba akcií 1 rok a 3 měsíce)

Roční výnosnost s reinvesticí výnosů se počítá na principu složeného úročení pomocí vzorce

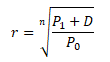
Odhad výnosnosti a rizika akcie ex post

Střední hodnota výnosnosti akcie je odhadována pomocí prostého aritmetického průměru, který měří průměrnou historickou výnosnost akcie za dobu držení T

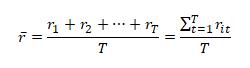
Riziko akcie (a jiných investic) je běžně odhadováno pomocí směrodatné odchylky na základě historických výnosů. Směrodatná odchylka (σ) měří riziko, které vyplývá ze změny (kolísání) výnosnosti akcie. Jedná se o druhou odmocninu z rozptylu a vyjadřuje průměrnou lineární odchylku výnosnosti od aritmetického průměru

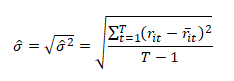
Riziko akcie měřené směrodatnou odchylkou představuje celkové riziko, které finanční teorie dále člení na systematické a jedinečné riziko. Jedinečné riziko souvisí s danou akcií a lze ho eliminovat diverzifikací cenných papírů. Systematické riziko nelze v rámci národní ekonomiky diverzifikovat. Je dáno ekonomickým systémem, ve kterém je akcie obchodována. V praxi se odhaduje pomocí koeficientu beta.

Anualizace výnosnosti a rizika akcie

Jestliže odhadujeme roční výnosnost a riziko z denních změn kurzu akcie, pak lze přepočet na roční veličiny provést jako 250·r a √250·σ. Číslo 250 představuje přibližně počet obchodních dní v roce.

Uvedené přepočty jsou jistě velmi praktické, ale je potřeba s nimi pracovat opatrně. Může se totiž stát, že jsou denní relativní změny kurzu akcie počítány z několika málo ziskových (ztrátových) nebo volatilních dní a převodem na roční hodnoty získáme nesmyslné informace. Lze se tomu vyhnout výpočty z maximálně dlouhé časové řady denních změn.

Výpočet výnosnosti a rizika akcií v praxi

Akciový trh je reprezentován hodnotově váženým indexem. Index je vážen tržní kapitalizací 5 kótovaných společností - akcie A (30 %), akcie B (12 %), akcie C (8 %), akcie D (21 %) a akcie E (29 %). Od zdanění a transakčních nákladů je abstrahováno.

Úkolem je vypočítat míru výnosnosti a rizika vybrané akcie a tržního indexu.

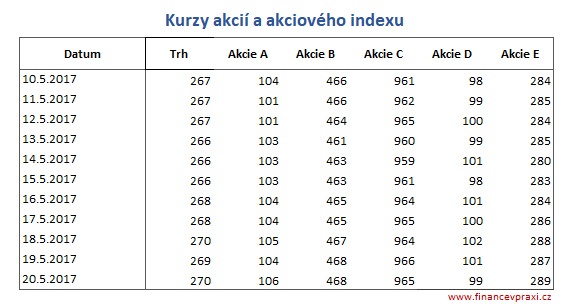
Na základě tržních cen akcií a akciového indexu jsou vypočteny denní změny v %. Z nich jsou vypočteny součty denních výnosností, průměrné denní výnosnosti, rozptyly, směrodatné odchylky a variační koeficienty.

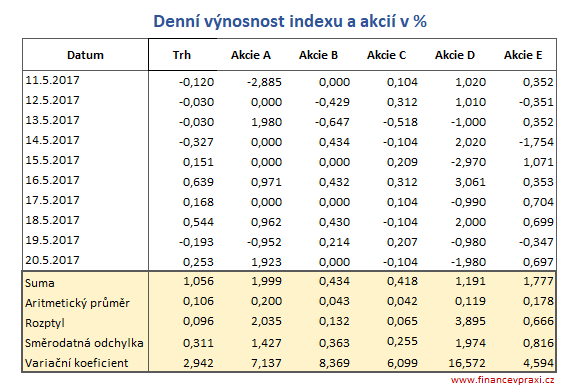
Výpočet denní a roční výnosnosti akcie B

Výpočet denní výnosnosti akcie B

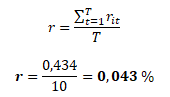
a roční výnosnosti akcie

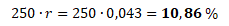
Výpočet rizika akcie B - rozptyl a směrodatná odchylka

Rozptyl denní výnosnosti akcie B

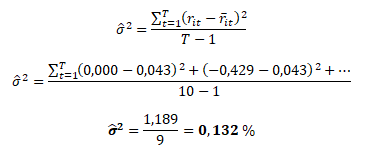
směrodatná odchylka výnosnosti

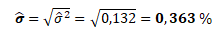
a roční rizikovost akcie

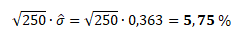
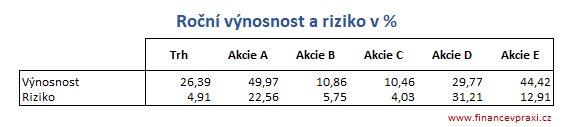
Následující tabulka obsahuje anualizované výnosové míry a míry rizika pro jednotlivé akcie uvažované v rámci modelového portfolia.