Odhad regresního modelu LINREGRESE()

V jednom z předchozích článků byly představeny excelovské funkce INTERCEPT() a SLOPE(), které se používají k odhadu parametrů regresní přímky. Uvedené funkce nejsou jediné, kterými můžeme odhadnout parametry regresního modelu. Další funkcí a v ekonometrické praxi jistě využívanější je maticová funkce LINREGRESE().

Funkce LINREGRESE() umožňuje rychlý a snadný odhad regresního modelu v Excelu včetně testů statistické verifikace modelu.

Funkce LINREGRESE()

Funkce spadá do kategorie statistických funkcí. Vrací odhady parametrů lineárního regresního modelu pomocí metody nejmenších čtverců.

Velkou výhodou funkce je navíc výpočet standardních chyb parametrů, koeficientu determinace, F-testu atd., které se používají ke statistické verifikaci modelu [stat]. Další užitečnou předností je možnost odhadu modelu s/bez úrovňové konstanty [b].

=LINREGRESE(pole_y; [pole_x]; [b]; [stat])

Funkce LINREGRESE() je maticová funkce, která vrácí výsledky do 5 řádků a n sloupců. Počet sloupců závisí na počtu parametrů v modelu. Výpočet maticového vzorce se provádí pomocí klávesy F2 a trojkombinací kláves CTRL + SHIFT + ENTER.

Funkci LINREGRESE() lze použít pouze pro modely, které jsou lineární v parametrech. Nelineární modely lze linearizovat například pomocí logaritmické transformace.

Funkce LINREGRESE() v praxi #1

Prvním příkladem je notoricky známá spotřební funkce spotřebitele. Pomocí jednoduché spotřební funkce je odhadnuta lineární závislost průměrných spotřebních výdajů y a průměrného měsíčního příjmu x v jednotlivých letech. Jednoduchá spotřební funkce má tvar lineárního polynomu prvního stupně Y = b₀ + b₁x.

Parametry funkce b₀ a b₁ odhadneme pomocí funkce LINREGRESE(). Pole hodnot závisle proměnné a pole hodnot nezávisle proměnné jsou barevně zvýrazněny v tabulce. Parametr úrovňové konstanty a parametr testovacích statistik jsou nastaveny na hodnotu PRAVDA.

=LINREGRESE(pole_y;pole_x;PRAVDA;PRAVDA)

Vyrovnané hodnoty spotřebních výdajů Y jsou vypočteny v následující tabulce pomocí regresního modelu Y = 21,951 + 0,446x.

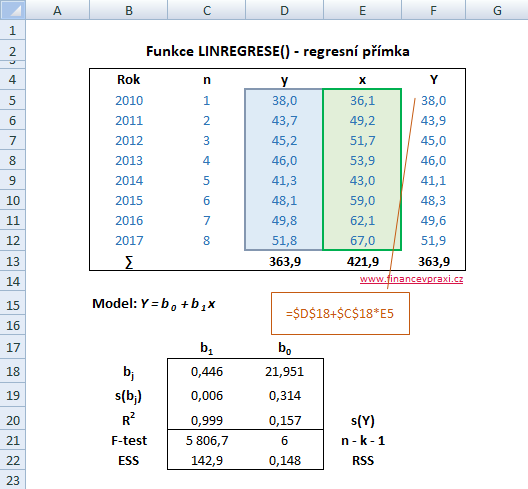
Zkratka b_j ve výstupu funkce představuje odhady parametrů modelu, s(b_j) jsou standardní chyby odhadu parametrů, R² je koeficient determinace, F-test je test průkaznosti modelu, ESS je rozptyl vyrovnaných hodnot závisle proměnné, RSS je rozptyl reziduální složky modelu, s(Y) je standardní chyba odhadu Y a n - k - 1 je počet stupňů volnosti. K vysvětlení uvedených pojmů doporučuji článek Testování regresního modelu.

Použití maticové funkce

Úkolem je odhadnout model s úrovňovou konstantou a testy statistické verifikace modelu. Prvním krokem je vložení funkce do vybrané buňky včetně výběru oblastí empirických dat. V druhém kroku jsou nepovinné parametry [stat] a [b] nastaveny na hodnotu PRAVDA. Dále označíme pole buněk o velikosti 5 x 2, přičemž v levém horním rohu výběru je buňka s vloženou funkcí. Stiskem klávesy F2 a poté trojkombinací kláves CTRL + SHIFT + ENTER máme hotovo.

Na následujícím grafu jsou proloženy skutečné hodnoty závisle proměnné y vyrovnanými hodnotami Y, které představují regresní přímku. Vysoká hodnota koeficientu determinace R² a vyrovnané hodnoty v grafu potvrzují velmi těsný vztah.

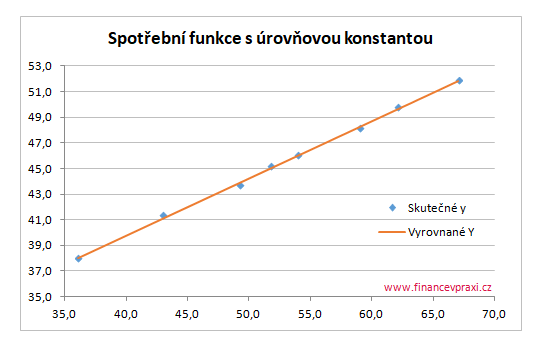
Srovnejte výsledky s odhadem modelu v článku Regresní přímka a Cramerovo pravidlo.

Funkce LINREGRESE() v praxi #2

Nyní využijeme možnost, kterou nám funkce nabízí a odhadneme spotřební funkci bez úrovňové konstanty ve tvaru Y = b₁x. Třetí parametr funkce, který se týká úrovňové konstanty, je nastaven na hodnotu NEPRAVDA.

=LINREGRESE(pole_y;pole_x;NEPRAVDA;PRAVDA)

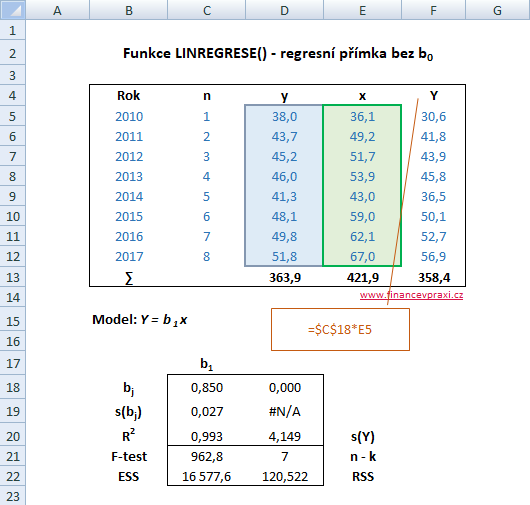
Koeficienty determinace obou spotřebních funkcí jsou vysoké. Nicméně reziduální součet čtverců RSS je u varianty s úrovňovou konstantou výrazně menší. Tento fakt je dobře viditelný i graficky. V první variantě jsou body těsněji proloženy regresní přímkou.

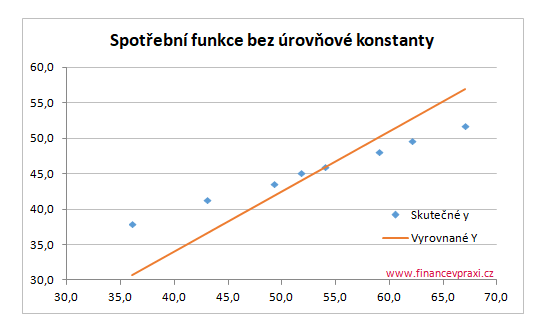
Graf modelu bez úrovňové konstanty vždy prochází počátkem. Kdyby byl příjem roven nule, byla by nulová i spotřeba. Osy grafu jsou záměrně omezeny na vyšších hodnotách.

Funkce LINREGRESE() v praxi #3

Třetím příkladem použití funkce je odhad regresní paraboly ve tvaru Y = b₀ + b₁x + b₂x². Postup je identický jako v předchozím případě. V modelu jsou 3 parametry, proto je třeba při použití funkce označit pole buněk 5 x 3.

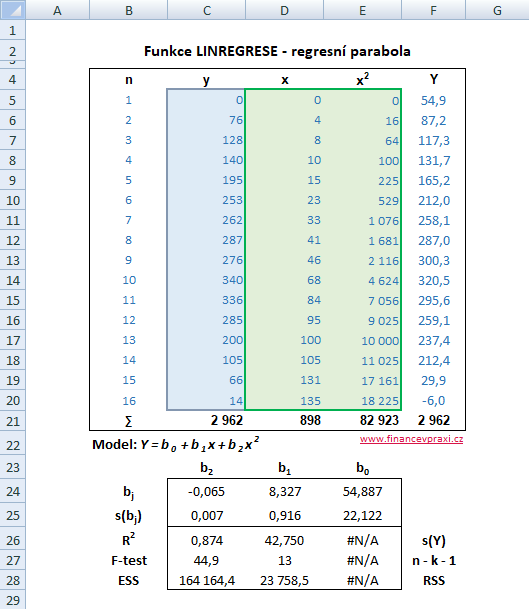
Na následujícím grafu jsou proloženy skutečné hodnoty závisle proměnné y vyrovnanými hodnotami Y regresní paraboly.

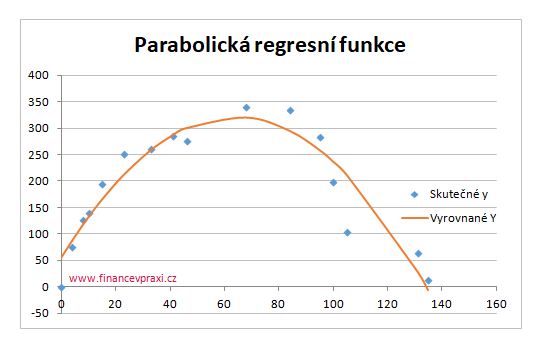
Srovnejte výsledky s odhadem modelu v článku Regresní parabola a Cramerovo pravidlo.